数位数制
在计算机科学中,有以下几种经常会用到的数制:
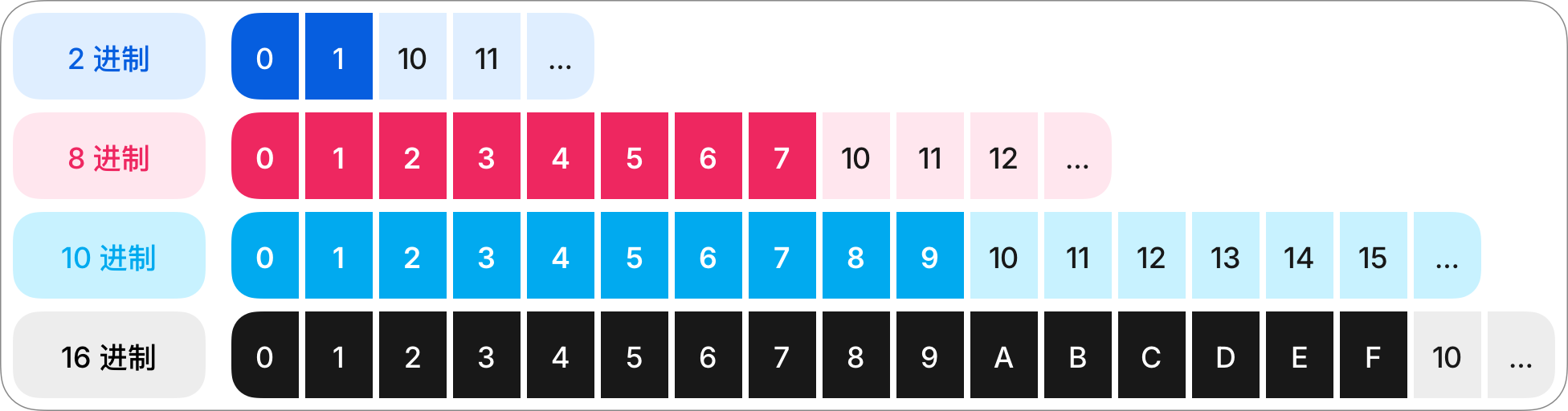
- 二进制 Binary(符号 B,逢二进一)
- 八进制 Octal(符号 O,逢八进一)
- 十进制 Decimal(符号 D,逢十进一)
- 十六进制 Hexadecimal(符号 H 或 0x,逢十六进一)
以上。
数制表示转化
二进制转十进制
二进制转十进制的计算方法为 各位值 \(\times\) 其位权。二进制各位的位权如下参考:

以将二进制的 10010.110 转为十进制为例,用上述公式可表达为:
$$
1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 + 1 \times 2^{-1} + 1 \times 2^{-2} + 0 \times 2^{-3} = 18.75
$$
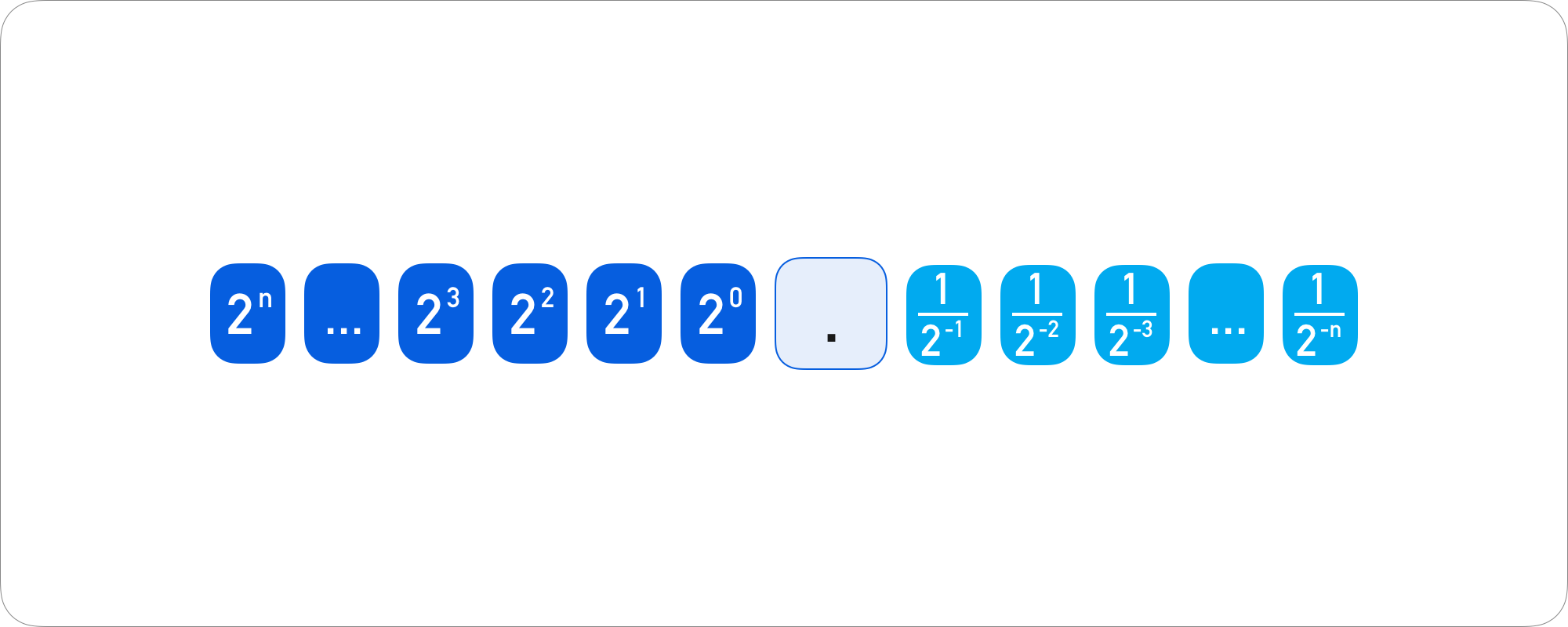
其中注意:若一个数的次方数小于 0 的计算方法为:先计算该数的倒数,然后求次方数的绝对值。在本次课中,可进一步简化记忆:计算小数点后的位权时,其位权可参考下图:
十进制转二进制
小数部分十进制转二进制
设十进制小数为 x,则将 x 乘以 2 并记录整数部分,剩下的纯小数部分继续乘以 2 记录整数部分,直到小数变为 0 或达到所需精度。以将十进制的 0.625 转为二进制为例:
| 步骤 | 当前值 \(\times\) 2 | 整数部分 | 小数部分 |
| 1 | \(0.625 \times 2 = 1.250\) | 1 | 0.250 |
| 2 | \(0.250 \times 2 = 0.500\) | 0 | 0.500 |
| 3 | \(0.500 \times 2 = 1.000\) | 1 | 0.000 |
计算得十进制的 0.625 = 二进制的 0.101。
二进制和八进制、二进制和十六进制转换
由于这三种进制的转换相对容易,因此我们将其一并讲解:
- 二进制转八进制
以小数点为中心向两侧转换,每 3 个二进制数为一组,每一组从左往右看,对应一个八进制数。不足的则补 0。 - 八进制转二进制
将八进制数的各数逐一转为二进制,每个八进制数可以转为一组 3 个二进制位的二进制数。 - 二进制转十六进制
以小数点为中心向两侧转换,每 4 个二进制数为一组,每一组从左往右看,对应一个十六进制数。不足的则补 0。 - 十六进制转二进制
将十六进制数的各数逐一转为二进制,每个十六进制数可以转为一组 4 个二进制位的二进制数。
十进制和八进制、十六进制的转换
先将初始数转为二进制数,然后由二进制数中转转为对应目标进制数。
特别注意
特别注意
部分小数位(例如十进制的 0.3)因进制逻辑差异,无法精确地转换为二进制数。
编码
在计算机中,常用的编码是 BCD 编码。即用 4 位二进制数来表示 1 位十进制数码。在 BCD 码中,我们常用的是 8421 编码:
| 十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 8421 编码二进制 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
| 十进制 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 8421 编码二进制 | 0001 0000 | 0001 0001 | 0001 0010 | 0001 0011 | 0001 0100 | 0001 0101 | 0001 0110 | 0001 0111 | 0001 1000 | 0001 1001 |
8421 码的加法运算
8421 码的加法运算是将两个 8421 编码的二进制数进行直接相加,相加后的值每 4 位为一组表示一个十进制数;若某一组不在映射表中,则需将这一组 +6(+0110)进行修正。
示例:求解 59 + 73
$$
\begin{eqnarray}
&\left \{ \begin{array}{l}
59 = 0101\ 1001 \\
73 = 0111\ 0011 \\
\end{array} \right. \\
\\
&1100&(9)\\
+&0011&(3)\\
= &1\ 0010&(12)\\
\\
&0101&(5)\\
+&0111&(7)\\
+&0001&(\text{进位})\\
=&1\ 1101&(13 \mathbb{{\color[RGB]{255,67,67}\text{[非法]}}})\\
+&0110&(6)\\
=&1\ 0011&\\
\text{则最终结果为:} &1\ 0011\ 0010\\
\end{eqnarray}
$$
这是因为十进制一个数位只有 0 – 9 共十个状态,而 8421 码的四个二进制数可以表示 16 个状态,故非法时 +6 将 10 – 15 这十五个十进制非法的数跳过进位到下一位继续计算。
ASCII 美国信息交换标准代码
ASCII 使用 7 位二进制编码来表示 128 中字符。该编码下所有大写字母、小写字母和数字的编码都是连续编码的。以下以 ASCII 的十进制编码为例进行说明:
- ASCII 中的 A
A 是大写字母连续编码的第一位,在 ASCII 中的编码为 65,其后 B 为 66,C 为 67…… - ASCII 中的 a
a 是小写字母连续编码的第一位,紧跟在大写字母 Z(96)后,在 ASCII 中的编码为 97,其后 b 为 98,C 为 99…… - ASCII 中的 0-9
0 是数字连续编码的第一位,在 ASCII 中编码为 48,其后 1 为 49,2 为 50……
在计算机中,所有字符以 ASCII 编码的形式存储于对应的存储单元中。例如已知一个字符存储在某存储单元中,题目若问该存储单元存放的内容是什么,则仅需求解该字符对应的 ASCII 编码的二进制形式并回答即可。
校验码
信息
校验码指能够发现或自动矫正错误的数据编码,它通过增加一些冗余码进行检验或纠错编码。
奇偶校验码
奇偶校验码通过在信息位后添加一位二进制位组成校验码。
- 奇校验码
整个校验码中有效信息位和校验位中 1 的个数为奇数。 - 偶校验码
整个校验码中有效信息位和校验位中 1 的个数为偶数。
简单理解为
在求某一段编码的奇偶校验码时,若求奇校验码,则确保原本编码+添加的奇偶校验码中所有 1 的个数为奇数;若求偶校验码,则反之确保所有 1 的个数为偶数。
例如求
1011010的奇校验码(设最高位为校验位),此时数其中 1 的个数:1 0 1 1 0 1 0
为 4 个(此时为偶数个 1),则需要在最左侧(最高位)添加 1 以让整个编码变为:
1 1 0 1 1 0 1 0
共 5 个 1(奇数个 1)。其它同理。
定点数
信息
定点数是小数点的位置在整个数值表示中是「事先约定、固定不变」,不随数值改变而移动。
- 定点整数
为纯整数,小数点在所有数值位的最右边(一般隐藏不显示)。
- 定点小数
为纯小数,所有有效数位都在小数点后,即所有数值都表示小数。
原码, 补码, 反码, 移码
原、补、反、移码是一组计算机中最重要的编码。
原码和反码
原码用机器数的最高位表示数的符号(0 正 1 负),其余位表示数的绝对值。反码的正数部分与原码相同,负数部分原码的符号位不变,其余数值部分全部取反(即 0 1 互换)。
例如对于 +213 这个数的表示,如下图所示:
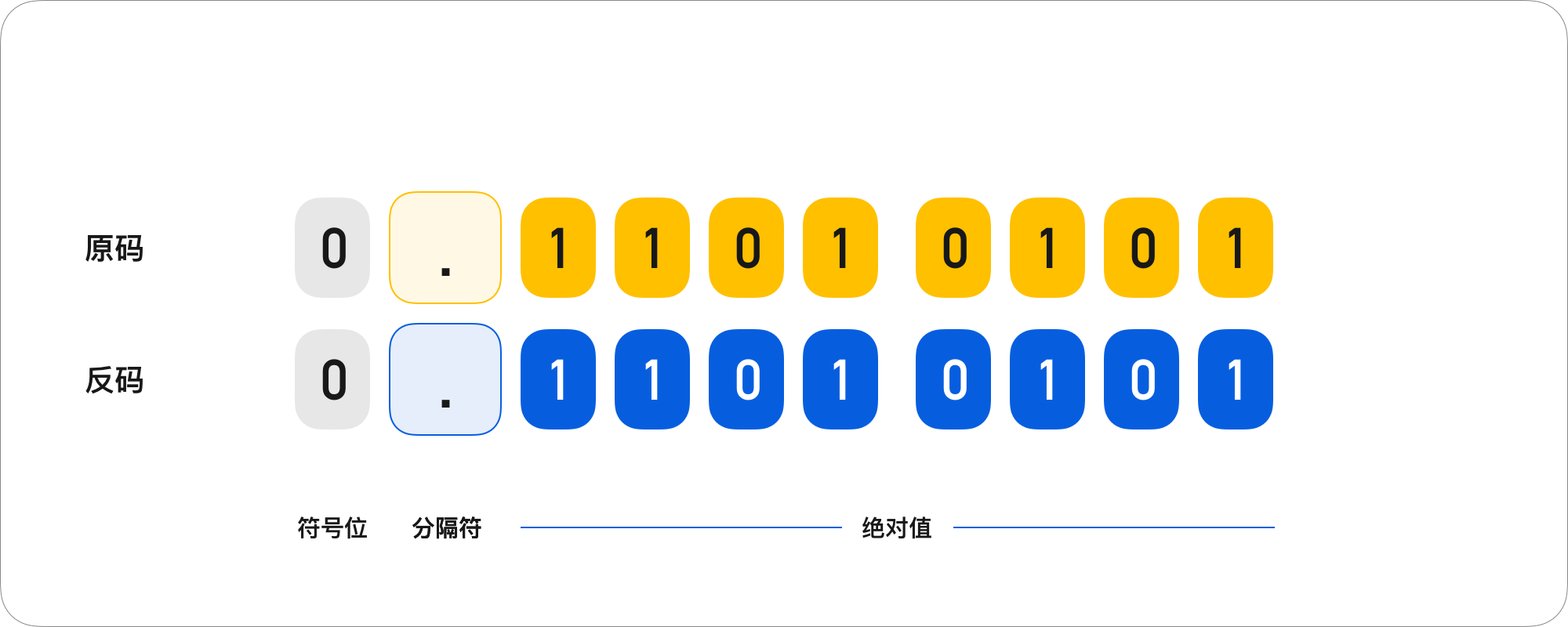
而对于 -169 这个数的表示则如下图所示:
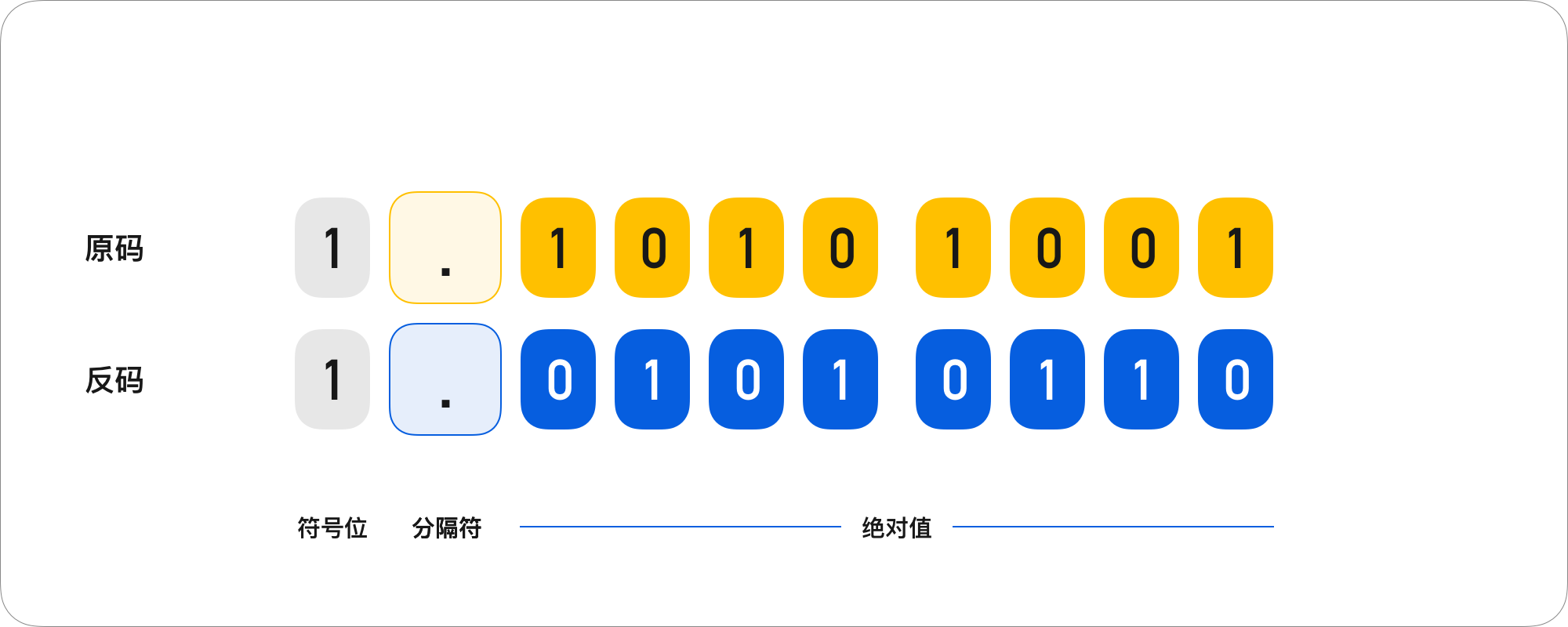
特别注意
真值为 0 的表示在原码、反码中各有两种,共三种:[+0]原反 = 0,000 、[-0]原 1,000、[-0]反 1,111
补码和移码
对于正数,补码与原码相同。对于负数,原码的符号位不变,其余数值部分全部取反并在末尾(一般为最右侧)加 1。此方法亦可反过来求负数补码的原码:末位 -1,然后取反得到负数补码的原码。
例如上图中原码 1, 1010 1001 的补码为 1, 01010111
移码是由补码的符号位取反得到。移码仅可用于表示定点整数。
特别注意
真值为 0 的表示在补码、移码中各仅有一种:[0]补 0,000、[0]移 1,000
浮点数表示
浮点数用于解决定点数「范围大没精度,精度高范围小」的问题。其核心思想是像科学计数法一样用「\(\text{尾数} \times \text{基数}^{\text{指数}}\)」来表示数值:
$$\text{数值} = \text{尾数} \times 2^{\text{指数}}$$
一个典型浮点数由 3 部分组成:数符、阶码、尾数。
- 数符
确定待表示数的正负性。0 为正,1 为负。数符只管正负,不管大小。 - 阶码
指数部分,用来表示尾数的定点小数小数点移动位数。阶码决定数值范围。阶符是阶码的符号位,用于表示阶码的正负性。 - 尾数
尾数通常为定点小数,且尾数的原码最高位为 1(反码和补码的最高位为 0),表示有效数字本身部分。尾数决定数值精度。
例如一个尾数为 0.1001,则其十进制为:
$$\frac{1}{2} + \frac{1}{8} + \frac{1}{16} = 0.6875$$
一个十进制数 13.25,其二进制为 1101.01(此处 0.25 的二进制为 0.01,因为 \(2^{-2} = 1\frac{2^2} = 0.25\));将其规范为浮点形式为:
$$ 0.110101 \times 2^4 $$
IEEE 754 标准
根据 IEEE(电气电子工程师学会)754 标准,常用的浮点数格式为:
数符位于最左(最高)位,数符后是阶码部分,用移码表示;阶码后是尾数数值位,用原码表示。
因为尾数用原码表示,且最高位恒为 1,因此 IEEE 754 标准的单精度和双精度浮点数(float 和 double)采用隐含尾数最高数位(即隐藏表示尾数最高数位)方法以节约尾数位空间,多表示一位尾数。临时浮点数无隐含位。
阶码是以移码的形式存储的,阶码具有偏置值:单精度的指数位数为 8,偏置值 127;双精度的指数位数为 11,其偏置值为 1023。因此:
$$\text{阶码真值} = \text{阶码}E – \text{偏置值}$$
该种方式确保实际存储的阶码 E 为正,即一个浮点数的阶码区域不用占用符号位,节约存储空间和提高效率。