什么是偏导数?
偏导数,是指对一个已知的多元代数式其中一个自变量的导函数,表示该函数在该方向上的变化率。若要计算偏导数,其方式为将除待求偏导的自变量之外的其它自变量视为常数,而后对该自变量进行求偏导。
【例】对函数 \(f(x,y) = x^2e^y + \arctan \frac{y}{x}\) 求偏导数并计算 \(f_x(1,0)\)。
要求 \(f_x(1,0)\),则需先求偏导数 \(\frac{∂f(x,y)}{∂x}\):
$$
\begin{array}{l}
\frac{∂f(x,y)}{∂x} = 2x \cdot e^y + \frac{1}{1 + {(\frac{y}{x})}^2} \cdot (-\frac{y}{x^2}) \\
\frac{∂f(x,y)}{∂x} = (2xe^y – \frac{y}{x^2+y^2}) \\
f_x(1,0) = 2
\end{array}
$$
当然,对于上面例题中提到的计算偏导数后求值类型的题,我们也可以使用另一种更简单的办法:先代后算。
以本题为例,因为题目要求求 x 偏导数,故原函数中的 y 对求偏导的结果没有影响;因此我们可以先将 \(y=0\) 代入到原式中,我们可以看到:\(e^y = e^0 = 1\),且 \(\arctan \frac{y}{x} = \arctan \frac{0}{x} = 0\),因此原函数化简为:
$$f(x,0) = x^2$$
然后计算偏导数,轻易可以得出 \(f_x = 2x, f_2 = 2\) 结果。
全微分
全微分,是指对一个多元代数式的每一个变量分别求偏导数,最后用加法连在一起。
【例】求 \(z = \arctan \frac{y}{x}\) 的全微分
全微分计算公式为 \(dz = \frac{∂z}{∂x}dx + \frac{∂z}{∂y}dy\)
即对代数式 z 中的 x 和 y 分别求偏导数,并用 + 连接。根据 \(\arctan x’ = \frac {1}{1 + x^2}\) 以及复合函数求导法则 \(f'(g(x)) = g'(x) \cdot f'(g(x)) \),全微分计算答案如下:
$$ \begin{array}{l}
dz = \frac{∂z}{∂x}dx + \frac{∂z}{∂y}dy\\
dz = \frac{1}{1+(\frac{y}{x})^2} \cdot (-\frac{y}{x^2})dx + \frac{1}{1+(\frac{y}{x})^2} \cdot \frac{1}{x}dy\\
dz = -\frac{y}{x^2+y^2}dx + \frac{x}{x^2+y^2}dy
\end{array}
$$
复合函数求偏导
原则:先画出关系链,同路相乘,不同相加。
【例】设 \(z = u^2\ln{v}\),其中 \(u = \frac{x}{y},\ v = 3x – 4y\),求 \(\frac{∂z}{∂x},\ \frac{∂z}{∂y}\).
对于本题,可以将对 x 和对 y 的偏导数分开来看。首先看如何对 x 求偏导数。根据 同路相乘,不同相加 原则,画出了如下关系图:
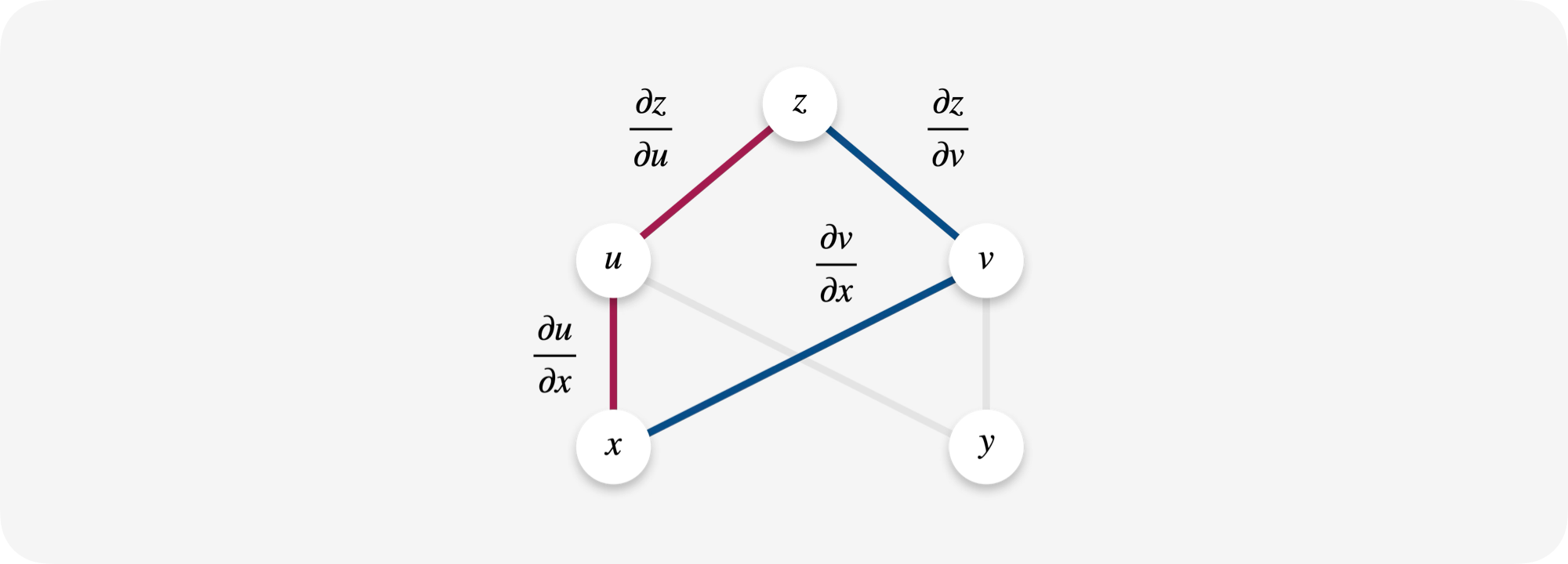
由图可得,求 z 沿 x 的偏导数为 \(\frac{∂z}{∂x} = \frac{∂z}{∂u} \cdot \frac{∂u}{∂x} + \frac{∂z}{∂v} \cdot \frac{∂v}{∂x}\).
代入原式可轻易得到 \(\frac{∂z}{∂x}\) 为:
$$\begin{array}{l}
= 2u\ln{v} \cdot \frac{1}{y} + \frac{u^2}{v} \cdot 3 \\
= \frac{2u}{y} \cdot \ln {v} + \frac{3u^2}{v} \\
= \frac{2x}{y^2} \cdot \ln{(3x-4y)} + \frac{3x^2}{y^2(3x-4y)}
\end{array}
$$
对于原式对 y 的求偏导数同理。
特别提示
对于没有明确给出 u、v 式子的抽象函数,例如 \(z = f(x^2-y^2,\ e^{xy})\) 中求对 x 和 y 的偏导数,我们可以先将 f 中被逗号分隔的式子分别定义为 u, v ,形成如下表达:
$$ z=f(u,v), \ u = x^2-y^2, \ v = e^{xy}$$
然后,由于 f 内部无法构成完整的式子,因此上文提到的 \(\frac{∂z}{∂u}\) 和 \(\frac{∂z}{∂v}\) 两个偏导数在书写结果时表达为 \(f_1’\) 和 \(f_2’\):
$$ \begin{array}{l}
\frac{∂z}{∂u} \cdot \frac{∂u}{∂x} + \frac{∂z}{∂v} \cdot \frac{∂v}{∂x} \\
= f_{1}’ \cdot 2x + f_{2}’ \cdot ye^{xy}
\end{array}
$$
多次求导
若需要对一个复合函数进行多次求导,谨注意一条原则:对于抽象函数中第一次求偏导数时产生的 \(f’_1, \ f’_2, \ f’_3 , \ \dots\),在接下来的求偏导数时,我们将其视为与 f 在同等的关系图位置:
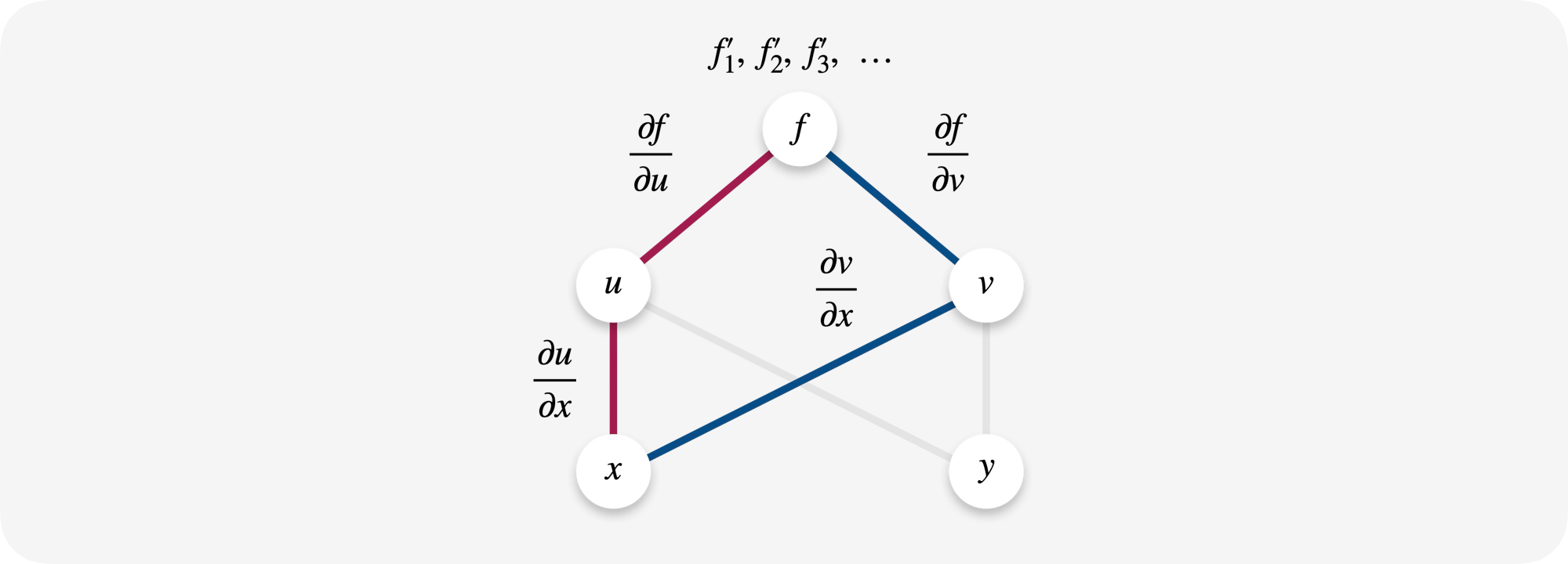
与第一次求偏导相似地,我们将 \(f’_1\) 等变量对 u、v 等抽象函数变量求偏导的结果书写为 \(f”_{11}, \ f”_{12}, \ f”_{21}, \ f”_{22}\) 等。
注意,因为题目中写有 f 具有二阶连续偏导数,说明 \(\frac{∂^2z}{∂x∂y} = \frac{∂^2z}{∂y∂x}\);因此最后求完二阶偏导数后的式子中, \(f”_{12}\) 和 \(f”_{21}\) 必须合并。
隐函数求偏导
隐函数是一种特殊的函数,例如 \(\sin{x} + 3y – z^3 – e^z = 6\),我们很难将任意一个自变量挪动到等号的另一边,形成 \(z = Ax + by\) 的格式。因此对于求隐函数的偏导数,我们可以分三个步骤实现它:
- 构造函数 \(F(x, y, z)\):
将题目给出的函数全部挪到等号的另一边,书写成 \( F = Ax + By + Cz + D \) 形式:
$$F = sin{x} + 3y – z^3 – e^z – 6$$ - 对代数式 F 分别求 x、y、z 的偏导数 \(F_x, \ F_y, \ F_z\):
$$
\left\{\begin{array}{l}
F_x = \cos x \\
F_y = 3 \\
F_z = -3z^2 – e^z
\end{array}\right.
$$ - \(\frac{∂z}{∂x} = -\frac{F_x}{F_z}, \ \ \ \frac{∂z}{∂y} = -\frac{F_y}{F_z}\):
$$
\left\{\begin{array}{l}
\frac{∂z}{∂x} = \frac{\cos x}{3z^2+e^z} \\
\frac{∂z}{∂y} = \frac{3}{3z^2+e^z}
\end{array}\right.
$$
MT の 特别提示
对于要求某函数在某点全微分具体值的题目,可用原函数获取函数所有变量的值 (x,y,z),并在第二步将值代入到 \(f_x, f_y, f_z\) 中,以降低在第三步时三个偏导数揉在一起的计算难度。