题型引航
已知双曲线方程求旋转曲面方程
【例】已知一双曲线方程如下,将其绕 X 轴转转一周,所生成的旋转曲面方程是? $$ 4x^2 – 9y^2 = 36 $$
解题技巧:绕谁转谁不变,另一个变为根号下的平方加平方。
在此式中,绕 X 轴则 X 不变,y 变为 \(\sqrt {y^2+z^2}\)。变化后带入得到: $$ 4x^2 – 9(y^2 + z^2) = 36 $$
【扩展】若本题为绕 Y 轴旋转,则 Y 不变,x 变为 \(\sqrt {x^2 + z^2}\) ,公式变为:$$4(x^2+z^2)-9y^2=36 $$
圆 \(x^2+y^2=r^2\) 在空间直角坐标系下表示
\(x^2+y^2=r^2\) 在平面直角坐标系表示一个圆,那么在空间直角坐标系下,因为 Z 轴不确定,则表示该方程在 Z 轴可以取任意值,也就是在 Z 轴上有无数个半径相等的圆。故 \(x^2+y^2=r^2\) 在空间直角坐标系下表示一个圆柱。
已知曲线,求其在 \(xoy\) 上的投影
$$\Gamma: \left \{ \begin{array} {l}
z = x^2+2y^2\\
z=2 – x^2
\end{array}\right.$$
已知曲线如上,那么其在 \(xoy\) 上的投影方程的计算方法为:
- 消去 Z。求其在哪两个轴上的投影,就消去另一个轴,得到一个相互等于的方程:
\(x^2 + 2y^2 = 2 – x^2\) - 化简后得到的即为投影方程:
\(x^2 + y^2 = 1\)
常用空间曲面:
请注意,此内容要求必背,且会画图。
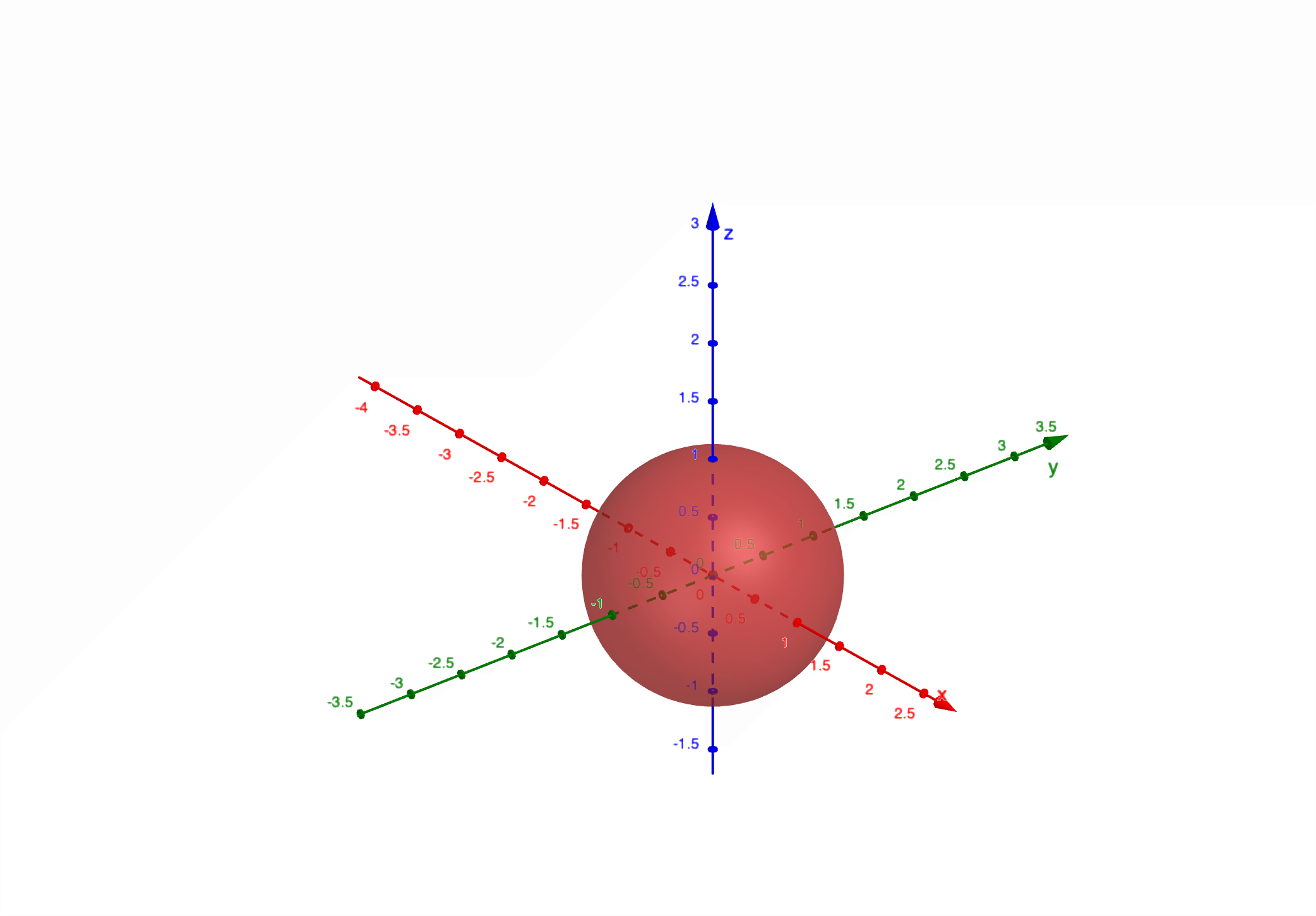
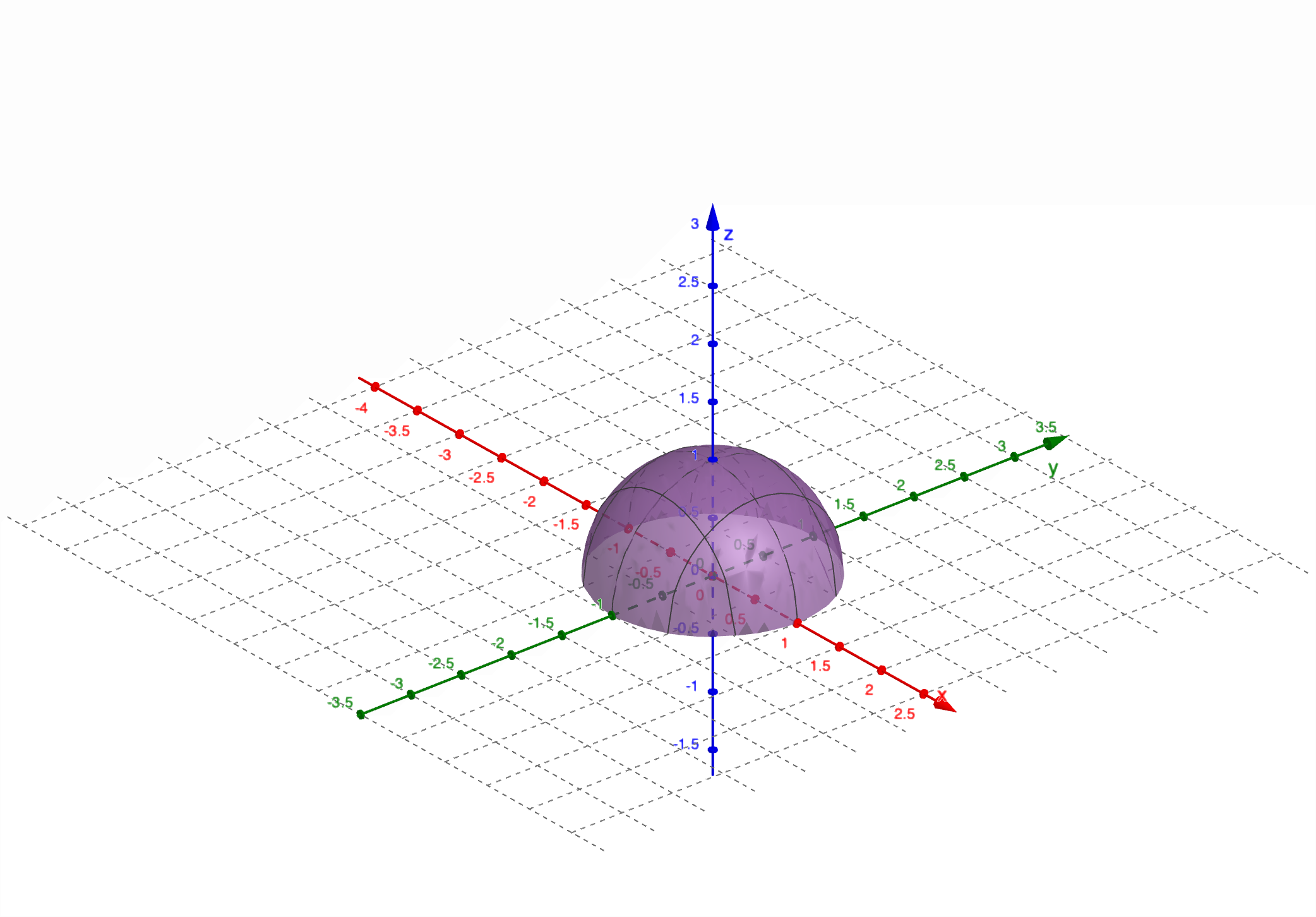
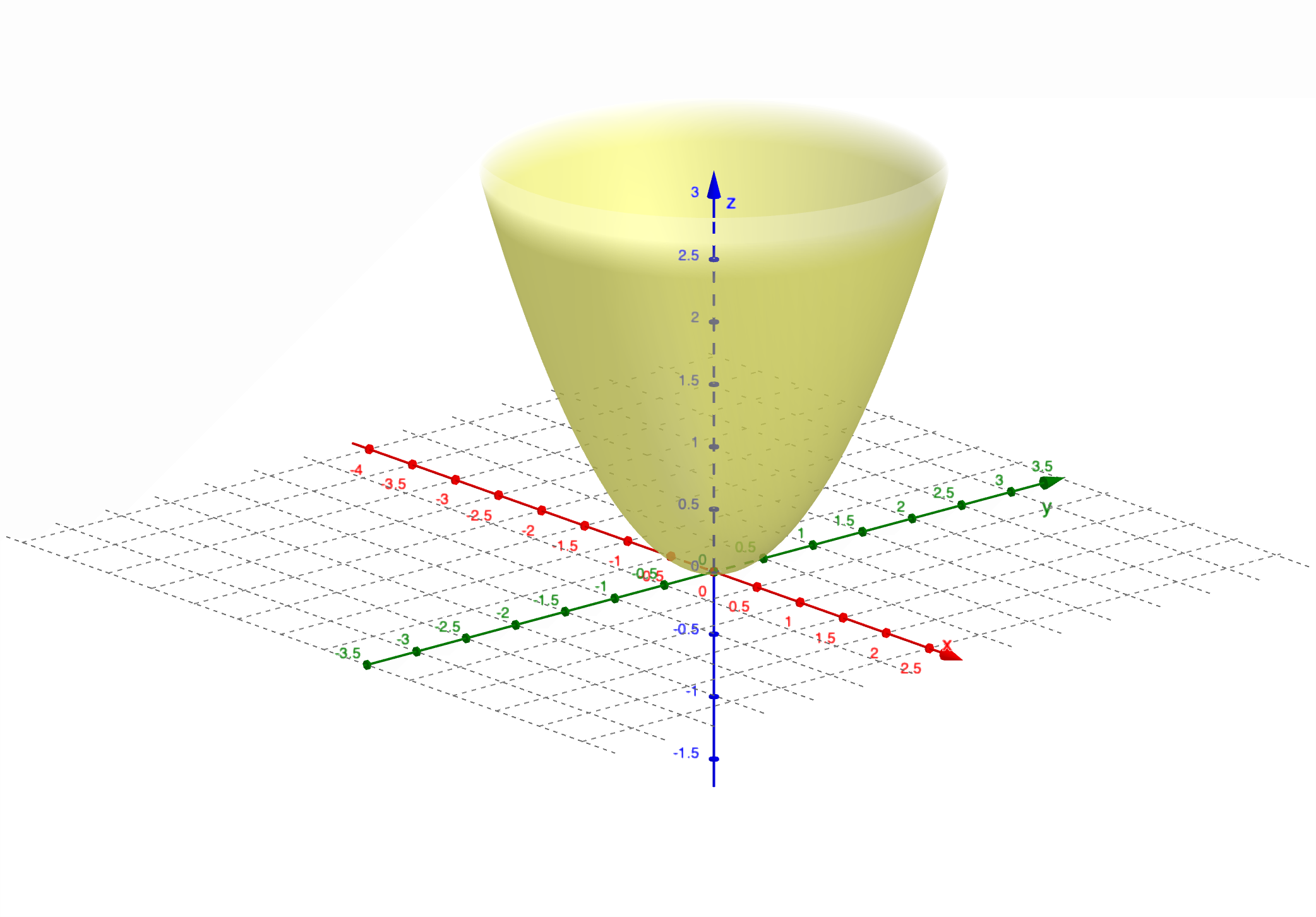
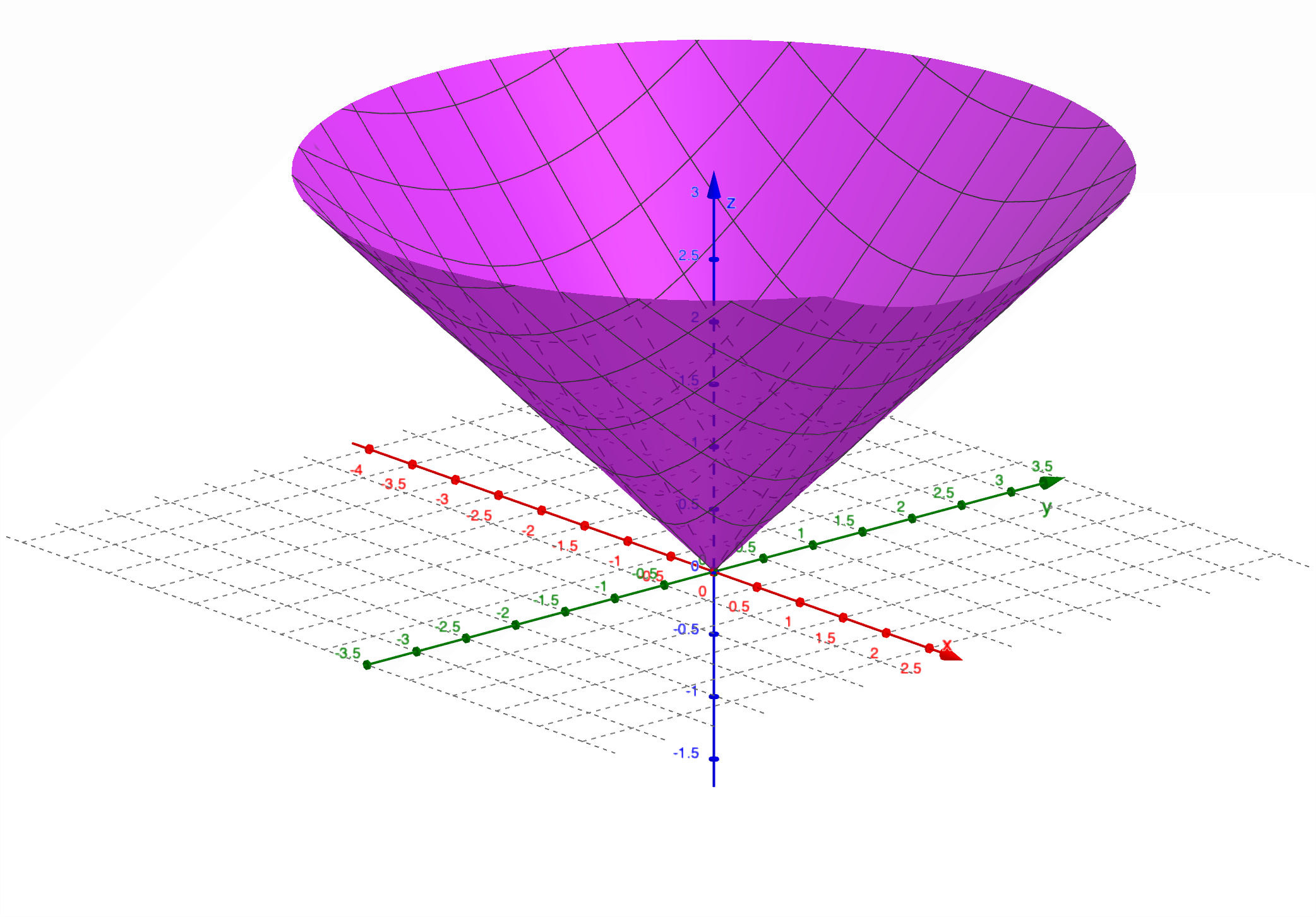
空间曲面的法线和切平面
有一空间曲面 \(f: z=x^(2)+y*2\),则任意垂直于该曲面的直线称为法线,任意与该曲面相切且只相切于一点的平面称为该曲面的切平面。
对于求切平面、法线,因为法线与法向量平行,且法向量垂直且过切平面,因此我们主要求法向量即可。以 \(2e^z-z+xy=4\) 在 \((2,1,0)\) 处的法线、法向量与切平面为例:
- 构造 F
首先将所有项移动到同一边,形成 \(2e^z-z+xy-4 = 0\) ,左侧即为 \(F: 2e^z-z+xy-4\). - 求偏导
对 F 的所有自变量分别求偏导数,并代入已知点的坐标值得到:\(F_x = y = 1, F_y = x = 2, F_z = 2e_z – 1 = 1\). - 获得法向量
则切平面的法向量(\(\vec n\)、法线的方向向量\(\vec s\) 即为\((1, 2, 1)\).
根据法向量和已知点,可以得到点法式方程:\(1 \cdot (x-2)+2(y-1)+1 \cdot (z-0)=0\).
根据法向量和已知点,可以得到法线的对称式方程:\(\frac{x-2}{1} = \frac{y-1}{2} = \frac{z}{1}\).
空间曲线的切线与法平面
对于一个曲线 \( x=t, y=2t^2,z=3t^2+1\),若求其在 t = 1 处的切线和法平面,我们同样可以以先求法向量(\(\vec s \& vec n\))为解题思路:
- 将 t=1 代入方程中,得到一个点坐标 \(P(1,2,4)\);
- 对原方程分别求导,随后将 t 代入导函数得到:
$$
\left \{\begin{array}{l}
x’ = 1 \\
y’ = 4t = 4 \\
z’ = 6t+1 = 7
\end{array}\right.
\Rightarrow
\vec s = \vec n = (1,4,7)
$$ - 由已知点和法向量,可以构造出切线的对称式方程和法平面的点法式方程:
$$\left \{ \begin{array}{l}
L: \frac{x-1}{1} = \frac{y-2}{4} = \frac{z-4}{7}\\
S: (x-1)+4(y-2)+7(z-4) = 0
\end{array} \right.$$
谨记:
- 若需要求空间曲面的法向量,我们可以将其整理后分别求 X、Y、Z 的偏导数,或是分别对 X、Y、Z 求导。将题目已知的点代入导函数方程,所得出的三个值即为法向量三个坐标轴方向的值。
- 当求出的对称式直线方程(\(\frac{x-x_0}{A} = \frac{y-y_0}{B} = \frac{z-z_0}{C}\))中,任意一个代数式的分母位为 0,那么其分子必定也等于 0(因为若分子不为 0,分母为 0,这个代数式没有意义)。例如上式子中,若 C 为 0,这个式子应当写为:
$$ \left\{\begin{array}{l}
\frac{x-x_0}{A} = \frac{y-y_0}{B} \\
z-z_0 = 0
\end{array}\right.
$$
666这么强