二重积分
直角坐标系的二重积分
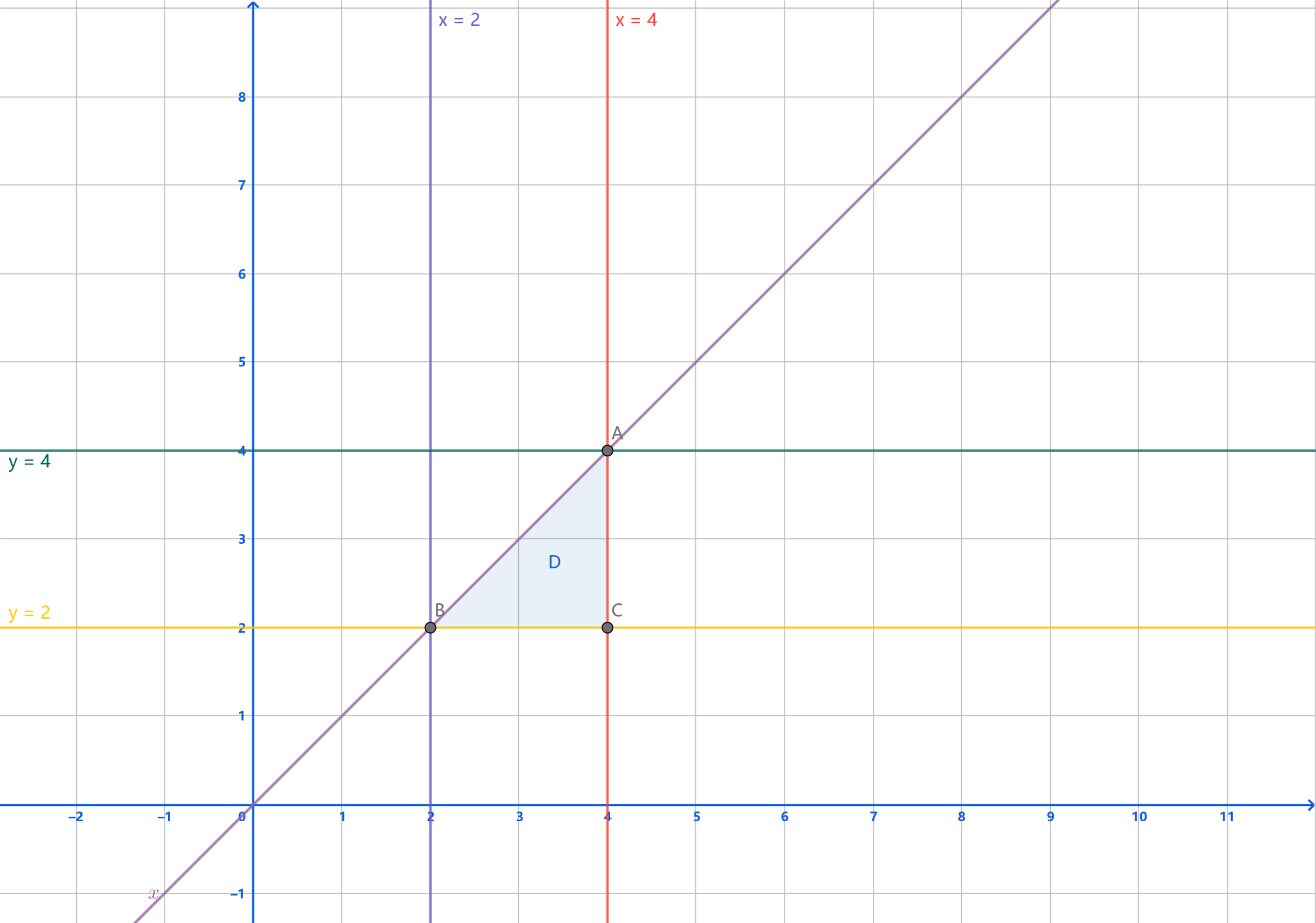
计算直角坐标系下的二重积分,首先要确定被求函数的积分界限(上下左右),随后拆分并分别对 X 和 Y 求积分。以求由函数 \(y=2, x=4, y=x\) 围成的区域 D 的二重积分\(\iint\limits_{D}xydxdy\)为例:
- 已知积分界限
对于容易画出图形的题目,画出图形中的三个函数及待求区域 D,可以简单确认 D 的下限和「右限」制为 \(y=2, x=4\) - 确定另外两个界限
根据图片,确定积分上限和「左限」为 \(y=x, x=2 \ \text{或} \ y=4, x=y\)(将斜线 y=x 构建为水平和垂直的界限)。则得到:X 的积分上限为 4,积分下限为 2,Y 的积分上限为 4,积分下限为 2. - 构建重积分公式
选择 X 或 Y 任意方便计算的一个方向,构建出如下函数:
\(\iint\limits_{D}xydxdy = \int_2^4 dx \int_2^x xydy \; \text{或} \; \int_2^4 dy \int_y^4 xydx\) - 从后往前计算重积分$$
\begin{eqnarray} \label{eq}
\int_2^x xydy &=& \frac{x}{2} \cdot y^2 \Bigg{|}_2^x \\
&=& \frac{x^3}{2} – 2x \\
\end{eqnarray} $$ - 计算最前积分得出结果
$$\begin{eqnarray} \label{ac}\int_2^4\frac{x^3}{2} – 2x dx &=& \frac{1}{8}x^4-x^2 \Bigg{|}_2^4 \\ &=& 16 – (-2) \\ &=& 18\end{eqnarray}$$
极坐标系的二重积分
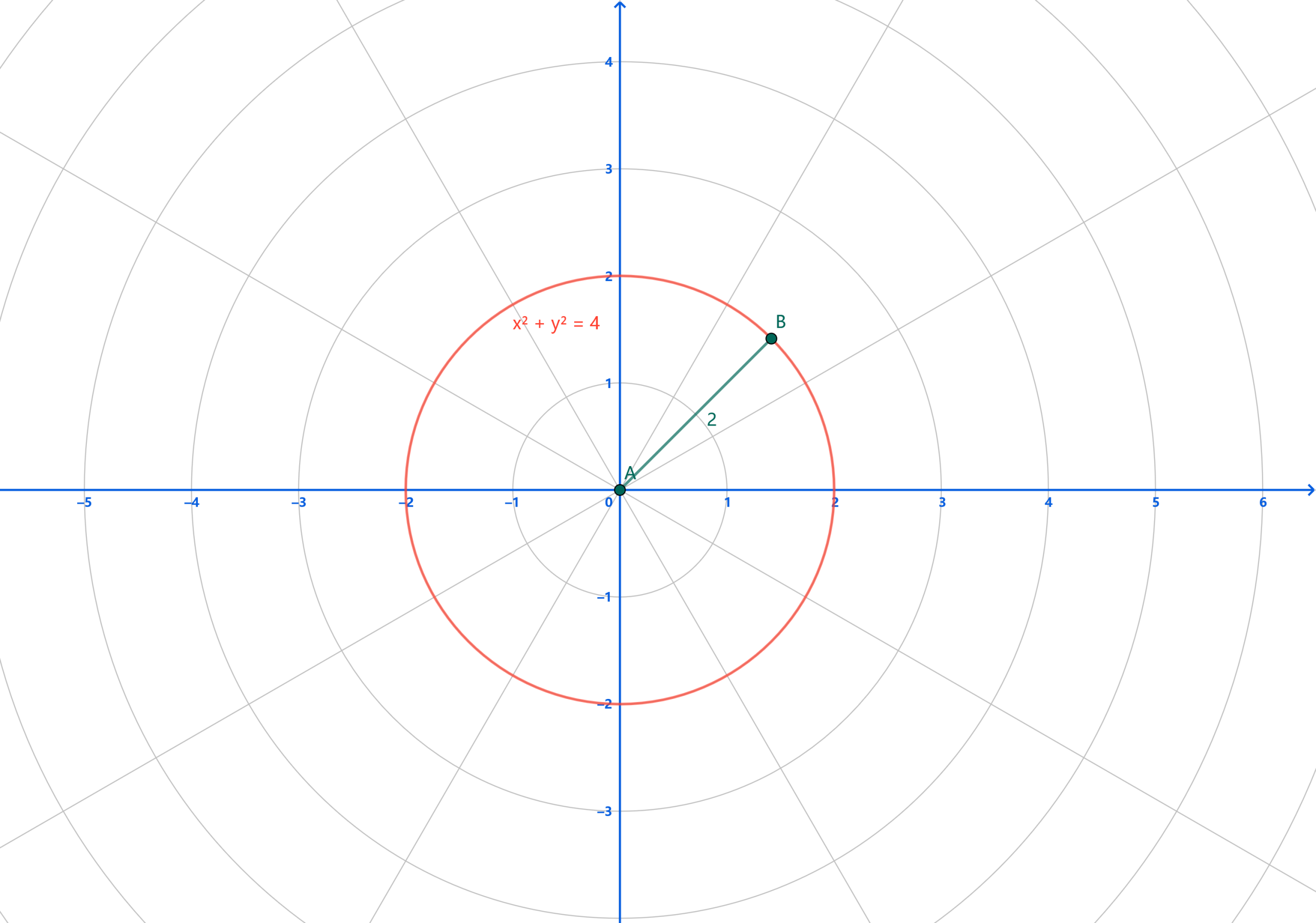
计算极坐标系下的二重积分,首先要确认定义 \(\rho , \theta\)的指代。\(\rho\) 指函数围成区域的半径,\(\theta\) 指待求积分区域从 y=0 沿原点旋转的角度。以求 \(\iint\limits_{D}\sqrt{x^2+y^2}dxdy, \; D:x^2+y^2\le 4\) 为例:
- 画出区域 D
- 确定 \(\rho\) 和 \(\theta\)
\(\rho = r : 0 \rightarrow 2\)
\(\theta : 0 \rightarrow 2\) - 利用简化公式计算
$$x = \rho\cos\theta$$
$$y = \rho\sin\theta$$
$$\sqrt{x^2+y^2} = \rho $$ - 构建重积分公式
构建重积分公式,并根据简化公式进行简化后,计算出重积分结果:
$$\begin{eqnarray} \label {13}
\iint\limits_{D}\sqrt{x^2+y^2}dxdy &=& \int_0^{2\pi} d\theta \int_0^2 \sqrt{\rho^2\cos^2\theta + \rho^2 \sin^2 \theta} \cdot \rho \ d\rho \\
&=& \int_0^{2\pi} d\theta \int_0^2 \rho \cdot \rho \ d\rho \\
&=& \int_0^{2\pi} d\theta \int_0^2 \rho^2 \ d\rho \\
&=& \int_0^{2\pi}\frac{8}{3} d\theta \\
&=& \frac{8}{3} \cdot 2\pi – \frac{8}{3} \cdot 0 \\
&=& \frac{16}{3} \pi
\end{eqnarray}$$
特别注意
请注意,对于 \(\theta\) 的范围确定,必须以圆心为起点旋转,且其旋转范围不应包括不存在图形的区域。
三重积分
直角坐标系的三重积分
$$\iiint\limits_\Omega f(x,y,z) dv$$
在上面的三重积分标准公式中:
- \(f(x,y,z)\) 为被积函数
- \(\Omega\) 为积分区域(体)
- \(dv = dxdydz\)
特别公式:截距式平面方程
若题目中存在一个平面方程为下面类似结构:
$$Ax+By+Cz = 1$$
那么这个方程也就可以通过系数变分母,化为如下结构:
$$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}$$
这个结构的平面方程的意思是:在空间直角坐标系中,该平面经过\((a,0,0), (0,b,0), (0,0,c)\) 三个点:
例题引航
计算\(\iiint\limits_{\Omega}(x+y)dv\),其中\(\Omega\) 为平面 \(x=0,y=0,z=0,x+y+z=1\) 在第一象限的部分。
- 画出立体图,确定 Z 上下面
由第三个公式 x+y+z=1 画出斜面,x=0,y=0,z=0 为 X、Y、Z 轴平面。
如下图可以确定,Z 的上表面为 \(x+y+z=1\),移项后得到 \(z=1-x-y\);Z 的下表面为 Z 轴所在平面 \(xoy\),即 \(z=0\).
综上:- \(z_{\text{上面}} = 1-x-y\)
- \(z_{\text{下面}} = 0\)
- 画出投影图,确定区域 D
即从上往下,将空间图形投影(压缩)为位于 \(xoy\) 平面上的图形。。
如下图确定(根据上文直角坐标系确定二重积分范围)可得:
X 的积分范围:\(x: 0 \rightarrow 1\)
Y 的积分范围:\(y: 0 \rightarrow -x+1\)
- 代入公式
以下是求三重积分的公式:
$$ \iiint\limits_\Omega f(x,y,z) dv =\int_{x_{\text{下限}}}^{x_{\text{上限}}}dx \int_{y_{\text{下限}} = f(x)}^{y_{\text{上限}}=f(x)}dy\int_{z_{\text{下限}} = z(x,y)}^{z_{\text{上限}}=z(x,y)}f(x,y,z)dz $$
将上文求出的 X、Y、Z 对应的积分上下限代入此公式,并将待求积分函数代入 \(f(x,y,z)\) 部分:
$$\text{原式} = \int_0^1dx\int_0^{-x+1}dy\int_0^{1-x-y} (x+y)dz$$
- 从后往前计算重积分
$$
\begin{eqnarray}
&& \int_0^1dx\int_0^{-x+1}dy\int_0^{1-x-y} (x+y)dz \\
&=& \int_0^1dx\int_0^{-x+1} (x+y)(1-x-y) dy \\
&=& \int_0^1dx\int_0^{-x+1} [-y^2+(1-2x)y+x-x^2] dy \\
&=& \int_0^1\Bigg[-\frac{1}{3}(1-x)^3+\frac{1}{2}(1-2x)(1-x)^2+x(1-x)^2\Bigg]dx \ \ \text{(对y积分后代入上下限)}\\
&=& \int_0^1(1-x)^2\Bigg[-\frac{1}{3}(1-x)+\frac{1}{2}(1-2x)+x\Bigg] dx\\
&=& \int_0^1(1-x)^2\Bigg[ \frac{-2(1-x)+3(1-2x)+6x}{6} \Bigg] dx\\
&=& \int_0^1\Bigg[ \frac{(1-x)^2(1+2x)}{6} \Bigg] dx\\
&=& \frac{1}{6}\int_0^1 (2x^3-3x^2+1) dx \Rightarrow \frac{1}{2}x^4-x^3+x\Bigg|_0^1=\frac{1}{2} \\
&=& \frac{1}{6} \cdot \frac{1}{2} \\
&=& \frac{1}{12}
\end{eqnarray}
$$
柱坐标系的三重积分
解题步骤(简要)
- 画立体图:确定 z 的下面和上面
- 投影图确定区域 D:确定 \(\theta\) 和 \(\rho\) 的范围
- 代入公式:
$$\iiint\limits_{\Omega}f(x,y,z)dv = \int_{\theta_1}^{\theta_2}d\theta \ \cdot \ \int_{\rho_1(\theta)}^{\rho_2(\theta)} \rho d \rho\ \cdot \ \int_{z_{\text{下}}(\rho\cos\theta, \rho\sin\theta)}^{z_{\text{上}}(\rho\cos\theta, \rho\sin\theta)}f(\rho\cos\theta, \rho\sin\theta,z)dz$$
其中:- \(x = \rho\cos\theta\)
- \(y = \rho\sin\theta\)
- \(\sqrt{x^2+y^2} = {\rho}
例题引航
计算 \(\iiint\limits_{\Omega} zdxdydz\),其中 \(\Omega\) 是由曲面 \(z=x^2+y^2\) 与平面 z=4 围成。
- 画图
由图易确定,Z 的上限为 z=4,Z 的下限为 \(z=x^2+y^2\)。将 X 和 Y 换为公式需求格式:
$$z: x^2+y^2 \rightarrow 4 \Rightarrow z: {\rho}^2 \rightarrow 4$$
- 画投影图
消除 Z:联立题目方程,得到:
$$x^2+y^2=4$$,此即为投影图形的方程,图形如下:
可轻易得到 \(\rho: 0 \rightarrow 2\) 且 \(\theta: 0 \rightarrow 2\pi\)
- 代入公式计算
$$
\begin{eqnarray}
\iiint\limits_{\Omega}f(x,y,z)dv &=& \int_{0}^{2\pi}d\theta \cdot \int_{0}^{2} \rho d \rho\cdot \int_{\rho^2}^{4}zdz\\
&=& \int_{0}^{2\pi}d\theta \cdot \int_{0}^{2} \Bigg(8 – \frac{1}{2}\rho^4\Bigg)\rho d \rho \\
&=& \int_{0}^{2\pi}d\theta \cdot \Bigg(4\rho^2 – \frac{1}{2}\rho^5\Bigg|^2_0\Bigg) \Rightarrow \int_{0}^{2\pi} \Bigg(16-\frac{16}{3}\Bigg) d\theta \\
&=& \int_0^{2\pi}\Bigg(\frac{32}{3} \Bigg)d\theta \\
&=& \frac{64}{3}\pi
\end{eqnarray}
$$
特殊性质
在三重积分的计算中,三重积分有以下性质可以提升解题速度:
- 若 \(f(x,y,z) = 1\)(即存在形如 \(\iiint\limits_{\Omega}dv\) 的式子),则\(\iiint\limits_{\Omega}dv = V\).
- 对称和奇偶性
- 若 \(\iiint\limits_{\Omega} f(x,y,z) dv\) 中 \(\Omega\)(待求积分的区域)关于 \(xoy\ /\ yoz\ /\ xoz\) 对称,且其中的 \(f(x,y,z)\) 关于任意坐标轴中心对称,则 \(\iiint\limits_{\Omega} f(x,y,z) dv = 0\)
- 若 \(\iiint\limits_{\Omega} f(x,y,z) dv\) 中 \(\Omega\)(待求积分的区域)关于 \(xoy\ /\ yoz\ /\ xoz\) 对称,且其中的 \(f(x,y,z)\) 关于任意坐标轴对称,则 \(\iiint\limits_{\Omega} f(x,y,z) dv = 2\iiint\limits_{\Omega’}f(x,y,z)dv\)
- 若积分区域 \(\Omega\) 关于 x,y,z 具有轮换对称性(x 换 y,y 换 z,z 换 x,\(\Omega\) 不变),则:
$$\iiint\limits_{\Omega}f(x)dv = \iiint\limits_{\Omega} f(y) dv = \iiint\limits_{\Omega} f(z)dv$$
此方法可以用于为 \(x^2\) 或 \(y^2\) 凑出 \(x^2+y^2\)。
球坐标系的三重积分
略