计算机组成原理｜数据的运算

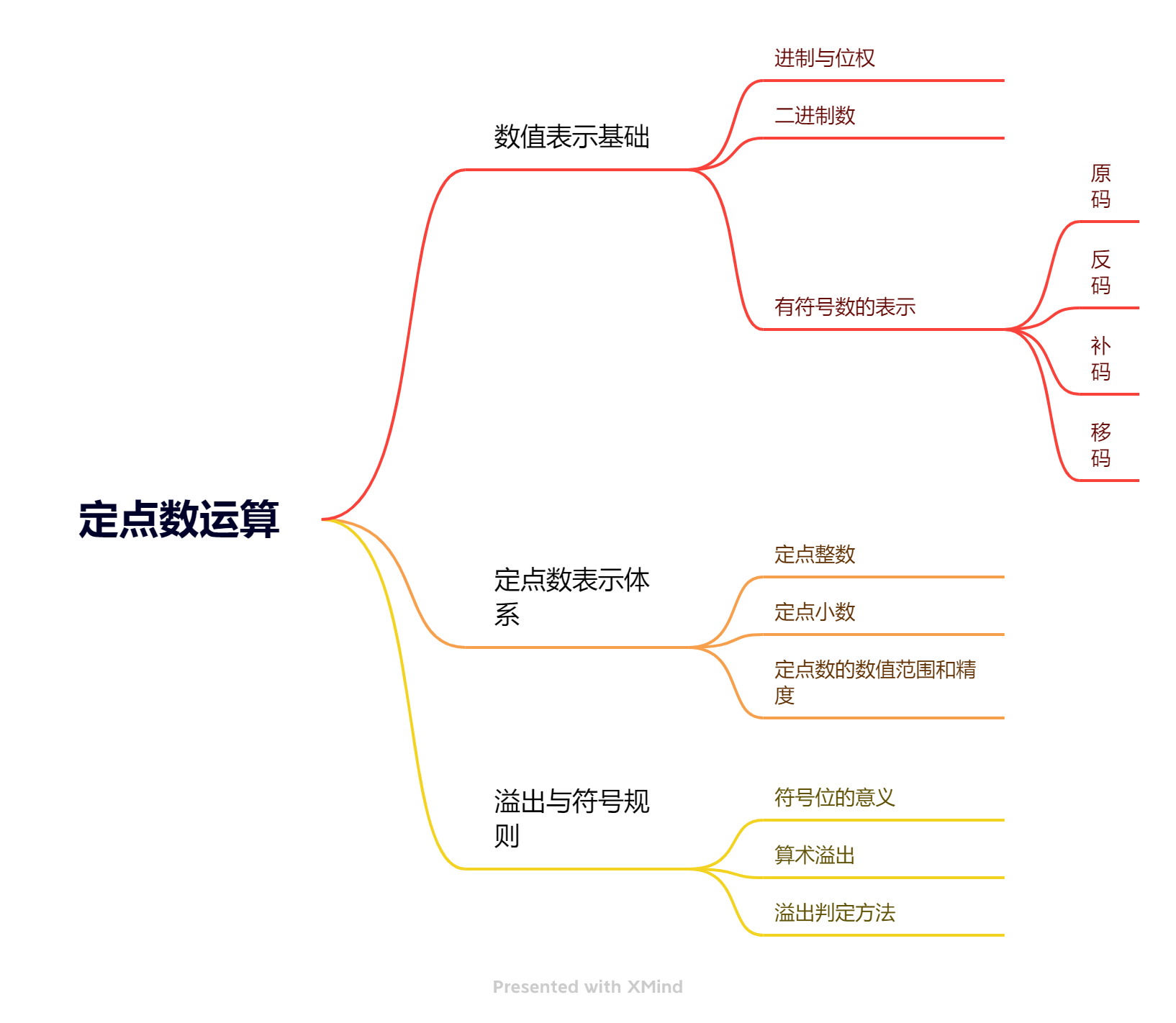
数值表示和定点数

有关本节的相关内容，可以参阅以下相关文章。

溢出与符号规则

基本移位运算

逻辑移位

逻辑移位运算不考虑数据符号意义，其包括逻辑左移和逻辑右移两种。移位运算是将当前数据整体向目标方向移动位置。无论逻辑左移还是逻辑右移，对移位后空出的位置一律补 0，对于被移数据移出位的数，无论其为 0 或 1 一律抹除。

循环移位

循环移位可以看作被移数据首尾相接形成环路，然后进行移位。无论循环移位左移或右移，被移出的数位自动填补到移后空出的位置。

溢出和算术移位

溢出是指运算结果超出数的表示范围。大于机器所能表示最大正数为上溢，反之为下溢。对于一个 n 位的补码，能表示的范围是 \([-2^{n-1},\ 2^{n-1}-1]\)。例如一个 8 位补码：

• 其所能表示的最小值是 1000 0000（-128），
• 其所能表示的最大值是 0111 1111（+127）。

加法溢出判定

符号位判定法

当两个操作数进行相加运算时，根据这两个数的符号相同与否来判定是否存在符号溢出。当两个操作数符号相同，结果符号不同时判定为溢出，两个操作数符号不同则一定不溢出。

操作数 A 符号	操作数 B 符号	结果符号	溢出判定
+	+	–	溢出
–	–	+	溢出
+	–	±	不溢出
–	+	±	不溢出

例如以下即为正溢出，两个正数相加超过了 8 位码所能表示的上限，数算溢出进位到符号位，导致计算结果为负数：

$$
\begin{array}{r@{\quad}r}
& 0111\ 0000_{2}\ \ &(+112_{10})\\
+& 0100\ 0000_{2}\ \ &(+64_{10}) \\
\hline
& 1011\ 0000_{2}\ \ &(-80_{10})
\end{array}
$$

以下为负溢出，两个负数（此处注意应使用补码（取反+1）运算）相加的结果超出 8 位表示上限，符号位溢出被抹除，导致计算结果为正数：

$$
\begin{array}{r@{\quad}r}
& 1001\ 0000_{2}\ \ &(-112_{10})\\
+& 1010\ 0000_{2}\ \ &(-96_{10}) \\
\hline
& 1\ 0011\ 0000_{2}\ \ &(\text{丢弃最高位}) \\
& 0011\ 0000_{2}\ \ &(+48_{10})
\end{array}
$$

减法溢出判定

减法的本质依然是加法，我们可以按照以下公式将减法运算递归回加法运算，以简化判定流程：

$$ A – B = A + (-B) $$

移位（乘除）运算溢出

移位运算可以看作是对二进制数据进行乘除 2 的运算。

算数左移的溢出

算数左移相当于这个二进制数在十进制位面进行 \(\times 2\)，但二进制字长不变。算数左移的判定方法为：若左移前后符号位发生变化，则判定为发生溢出。

等价说法

• 左移前最高两位不同
• 原符号位 \(\ne\) 新符号位

以下为例子：+64 的二进制补码（等于原码）进行左移时，数位最高位移入符号位，导致符号位发生变化，判定为溢出。

$$
\begin{array}{c}
+64 &=& 0100\ 0000 \\
\text{ASL} &\rightarrow& 1000\ 0000 &=& -128
\end{array}
$$

算数右移的溢出

算数右移时可看作是除法。原码符号位不参与数值，因此对于原码的负数部分最高位补 0；补码、反码的负数部分的算数右移最高位补 1。

总结

	码制	符号位	右移空缺位填补值	左移空缺位填补值
正数	原码、反码、补码	0	0	0
负数	原码	1	0	0
负数	补码	1	1	0
负数	反码	1	1	1

移位计算误差的舍入

移位计算的本质是对二进制数据进行乘除 2 的运算，但是定点整数（整数）的除法通常无法精确表示结果（截断误差）：

$$
\begin{array}{l}
\text{DEC} && {5\div 2} = 2.5 \\
\text{BIN} && 0101 \ \ (5)\\
& \text{ASR} \rightarrow & 0010\ \ (2)\\
\end{array}
$$

从上面的例子可以发现，误差由被移出的最低位（LSB）决定。当被移除位是 0 时（即这个二进制数是 2 的倍数），这个计算结果是精确的。当被移除位是 1 时，进行移位计算会丢失 \(2^{-1}\) 。因此常使用 0 舍 1 入法对这个误差进行舍入处理：

零舍一入法

在进行正数的右移移位计算时，若被移除的最左侧位为 1，则在移位结果的最低位加 1；若为 0 则不加。

进行补码负数的右移移位计算时，分为以下几种情况：

• 被移除的最左侧位为 0
  舍去。
• 被移除的最左侧位为 1
  • 被移除部分其余各位全部为 0
    舍去，且保留部分不变。
  • 被移除部分其余各位存在 1
    入，且对保留部分的最低为 +1（即 +2）

依然以 \({5 \div 2}\) 为例：

操作	数值	备注
	\(0101_2 = 5_{10}\)	原始值
右移（\({\div 0010_{2}}\)）	\(0010\)\(1\)\({_2} = 2\)	右移后最低位为 1
零舍一入	\(0011_2 = 3\)	最低位为 1，入

由上可以看出，零舍一入法实际可看作移位运算在二进制位面进行「十进制位面的小数部分四舍五入」处理。

定点数运算

定点数加减法

定点数的加减法以带符号位计算两个数值补码的形式进行。这里的定点数减法同样遵循 \(A – B = A + (-B)\) 的等价关系进行转换递归后计算求解。减法的本质是加上一个取负的数，因此这里主要讲如何进行定点数的加法。

1. 计算两个定点数加法，首先判断这两个数（设为 A 和 B）的状态：若为非补码，则将他们转化为补码。
2. 随后，将两个补码做加运算，得出计算值。
3. 若存在溢出，按照题目要求处理溢出（舍去、中止运算、不处理等）

定点数乘法运算

原码乘法运算

原码的乘法运算大体与常规十进制运算相仿，不同之处是计算的位权为 2。此外，在进行一切数据部分的数算之前，需要先计算符号位。记住：「同号为正，异号为负，例如在十进制中计算 \(45 \times 13\)：

$$
\begin{array}{r@{\quad}r}
& 45\
\times & 13 \\
\hline
& 135\\2
+& 4500 \\
\hline
&4635\\
\end{array}
$$

在二进制中计算 \(3 \times 5\)：

$$
\begin{array}{r@{\quad}r}
& 0000\ 0011\\
\times & 0000\ 0101 \\
\hline
& 0000\ 0011\\
& 0000\ 0000\\
+& 0000\ 1100 \\
\hline
&1100_2 (15)\\
\end{array}22
$$